My family vacations in Maine most years, and because it's so far north and east, the sun rises egregiously early around the summer solstice. I was looking up the sunrise times on a chart and noticed that the earliest sunrise did not line up with the longest day. It was about a week earlier. Additionally, the latest sunset is about a week after the solstice. At the winter solstice, the latest sunrise and earliest sunset are even further off, about two weeks in either direction from the solstice.
I thought that the math behind this calculation would make for good content for an article, but the true reason behind the anomaly is much more interesting than a simple calculation, and has significantly altered my understanding of time itself.
For nearly as long as life has existed on Earth, the idea of a day and night has been driven by the sun. The day starts when the sun rises, and at dusk, daytime ends and nighttime begins. Daytime is longer than night in the Summer, and shorter in the Winter. As the need arose for more exact timing throughout the day, we began to divide the day and night each into 12 segments called hours. The sixth hour would be solar noon, when the sun is highest in the sky. The apparent length of an hour would change throughout the seasons, as the length of daylight changed. This convention is called 'unequal' or 'temporal' hours1. As you can imagine, these hours would be difficult to measure mechanically, and so time-of-day was measured using devices which used the sun directly (sundial, etc). Timers were still helpful to measure durations, and so water clocks were used to measure more exact and reproducible durations2.
Historical Context
Around the 4th century BC, Babylonians began to use hours of equal length to measure the time of day and night3. This was done via measurements and calculations of the sun and stars using something like as astrolabe4. However, the complicated nature of using these meant that most people continued to casually use relative hours based on the position of the sun for timekeeping. This changed in the late 13th century with the invention of more precise mechanical clocks featuring an escapement5. By the late 14th century, hundreds of turret clock were installed in town squares all over Europe6. Many of these also kept track of the sun and stars with increasingly complicated mechanisms. These clocks ushered in a universal time that could be easily read by the entire town, even without a line-of-sight, as many featured chimes on the hour. The accuracy of these clocks improved greatly in the 17th century with the addition of a pendulum7.
Humanity moved away from the idea of clocks measuring a day, and towards the idea that a clock defines a day. Clocks became prescriptive, not descriptive. No longer does the day start when the sun rises, but rather the time of sun rise must be calculated and looked up. As clocks became more precise, they added a second hand, and removed the tracking of astronomical bodies. The severance of time from the cosmos was complete in 1967 when the International Bureau of Weights and Measures officially defined a second as the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom.8 The abstraction fully replaced the reality.
Time as an Abstraction
In his seminal work, Simulacra and Simulation (1981)9, French philosopher Jean Baudrillard speaks of a fable10 in which 'the cartographers of the Empire draw up a map so detailed that it ends up covering the territory exactly.' All resources are diverted towards the creation of the map, and so the Empire falls into decline and the map frays and falls into ruins. Baudrillard argues that modern civilization has created this map, but is actually the real territory which rots away and not the map. Society lives directly on the map, whose relationship to the territory is lost completely. He calls it 'The desert of the real.' (famously quoted in The Matrix11). Why don't our clocks match up with the sunrise? Does it even matter? Does anything matter? What even is time?
This is a rather existential explanation for what I originally thought was a math question, but it got me thinking about what other abstractions in our lives have replaced the territory beneath them:
- Music notes - The relationships between notes is based on ratios of the frequencies of the notes. However, the interval among the 12 notes in a scale is not equal, and so tuning an instrument can get complicated, as a single scale would have to be chosen for the tuning, and other scales would be off. The introduction of equal temperament12 'solved' this, by making all the intervals equal, even if it means they're a little off from the pure ratios. Sensitive ears can hear this difference13, but for the most part, equal temperament is what we hear in everyday music.
- Fiat currency - Money became more convenient than bartering, but was still based on something. The US used to have the gold standard, where the amount of US dollars in circulation was tied to the value of gold. In 1971, the US severed this link, and the US dollar is now basically based on itself14.
- Computer Code - If you're a coder, how often do you think about how your code actually runs? The answer is likely never. We are all multiple layers of abstraction away from the reality of the runtime.
- Maps - The fable about the map that covers the terrain is already happening in a way. I have, on more than one occasion, when trying to find parking rules for my neighborhood, used street view to read the sign rather than going outside. The terrain isn't rotting away yet, but it is being replaced, at least to a small degree, by it's abstraction.
The 'Answer'
Why does the earliest sunrise not align with the longest day? I had the question flipped. The question should actually be, 'Why is our clock time off from the sunrise in this way?' Beware, nerd stuff ahead:
There is an actual equation relating mean time to solar time15. It is the sum of two sine waves which represent:
- The change in tilt relative to the sun throughout the year
- The non-circularity of the Earth's orbit around the Sun
∆tey = 9.863 * sin(2D + 3.5932) - 7.659 * sin(D)
where D = 6.24004077 + 0.01720197(365.25(y - 2000) + n)
where n = day number of year
The resulting graph shows how a modern clock runs relative to days as defined by the difference between solar noons for each day:
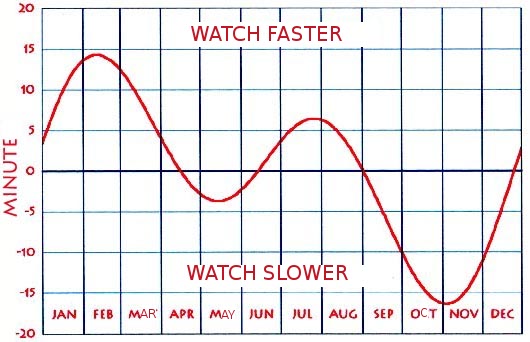
And for the actual answer to my original question:
Given the equation for the length of a day:
ts = 2/15 arccos (–tan φ tan δ)
where φ is the latitude and δ is the Sun's declination
The dates of earliest sunset and latest sunrise are the dates before and after the winter solstice when, at a given latitude, the magnitude of half the daily change in ts equals the magnitude of the daily change of the Equation of Time16.
Conclusion
Abstractions exist for a reason. They are generally easier to deal with than the underlying reality. It would be nearly impossible to schedule an international meeting if we all still used temporal hours. Retuning a piano for every song is not going to happen. However, let's not let the terrain rot under the map. Let's remember that the day begins at sunrise, and sometimes that's close enough.


